La física de los tiros libres

Todavía duele, ¿no?


donde:
D es el diámetro del balón en metros,
f la frecuencia de giro del balón,
V su velocidad.

La fórmula matemática del mortal tiro libre de David Beckham

Sin ninguna duda, David Beckham es un maestro de las ecuaciones diferenciales no lineales. Basta recordar aquel tiro libre con el que logró que Inglaterra clasifique a cuartos de final del último Mundial frente a Ecuador, o el tiro libre que anotó en un partido de eliminatoria a la Eurocopa 2004 ante Grecia. Mientras el resto de la gente se pasaba haciendo aviones de papel y jugando al ahorcado en clase, Spice Boy se dedicaba a comprender los finos detalles de los números de Reynolds, las fuerzas de Magnus y los coeficientes de arrastre aerodinámico.

Por supuesto, como todo genio, Beckham no desarrolló su talento en un lugar tan mundano como un salón de clases. Aprendió sus trucos para resolver ecuaciones pateando un balón unos cuantos millones de veces. Es cierto que cualquier físico conoce de memoria las ecuaciones que gobiernan la trayectoria de un tiro libre con comba, pero el ponerlas en práctica durante un partido real es un asunto totalmente diferente. Tal como otros grandes cañoneros con pelota parada (Roberto Carlos, Figo, Zola, Zidane), Beckham cambió las horas de física teórica por años de prueba y error sobre el gramado.

Para todos aquellos que nos conformamos con que el balón viaje en línea recta, también hay un beneficio en comprender la física detrás de aquellos impresionantes disparos, ya que nos hace apreciar más el impresionante talento de estos jugadores. Lo que ellos hacen raya en un milagro, optimizando tres fuerzas diferentes, dos de las cuales cambian constantemente cuando el balón está en vuelo.

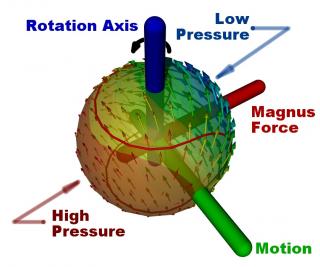
La primera fuerza es la que conocemos mejor: la gravedad. No hay mucho que descubrir aquí, dado que permanece constante. La segunda es mucho más difícil de cuantificar y manejar. Se la conoce como Fuerza de Magnus (en honor de H.G. Magnus, un físico alemán quien investigó por primera vez sus propiedades hace unos 150 años). Ésta es la fuerza directamente responsable por la curva que el balón realiza fuera de su trayectoria normal. A menos que el esférico sea impactado en su centro geométrico, siempre girará ligeramente mientras se mueve en el aire. Por el hecho que uno de los lados del balón está girando en la misma dirección que la trayectoria de vuelo, mientras que el otro gira en dirección contraria, existe una ligera diferencia en la velocidad relativa del aire en cada costado. Esto crea, en consecuencia, una diferencia de presión que hace que la bola se mueva en una curva en vez de en una línea recta. La regla cardinal dicta que se debe patear el costado izquierdo del balón para darle un giro en contra de las agujas del reloj (visto desde arriba), y curvará hacia la izquierda.



La premisa puede sonar simple, excepto que hacer que el balón salga con "chanfle" no es suficiente. Debe curvar de modo preciso, y aquello no sólo depende del giro, sino también de la velocidad del objeto en el aire. La fuerza del disparo debe ser perfectamente calculada, para optimizar el giro y la velocidad.

Con algo de práctica, incluso el típico deportista dominguero tiene la oportunidad de mandar un balón con "comba" al fondo de las piolas. El verdadero talento surge cuando se tiene que superar también a la barrera de defensores. He ahí donde los maestros muestran su dominio de la tercera fuerza en juego al disparar un tiro libre: el arrastre aerodinámico. Tal como las fuerzas de Magnus, la fuerza de arrastre cambia con la velocidad del balón. El problema radica en que esta fuerza cambia de manera mucho más aleatoria y abrupta, haciéndola mucho más difícil de controlar. Además, esta fuerza influye críticamente la magnitud de la fuerza de Magnus, y por ende, el modo en el que el balón curva.

La solución obvia para esto sería disparar el balón con la misma fuerza todas las veces, y tratar de enfocarse en controlar el giro, pero para un genio de la pelota parada, el arrastre ofrece una manera manejable de engañar a la barrera y al arquero al mismo tiempo. Si se golpea al balón fuertemente en uno de sus costados, por ejemplo a unos 110 km/h, el balón empieza a volar lejos de la barrera, con poco arrastre y sin esperanza de entrar en el arco. Los defensores se relajan, y el arquero se burla para sus adentros de la incapacidad de su oponente. Sin embargo, cuando el balón va perdiendo su impulso inicial, el arrastre aumenta rápidamente, junto con la fuerza de Magnus, causando que el balón curve aún más pronunciadamente. De repente, el arquero ve el balón curvando en dirección al segundo palo, y antes que pueda llegar a ella, el balón se mete en el arco.

Según algunos cálculos científicos, puede haber un desvío de hasta 4,6m (5yd)en un tiro libre a unos 23m (25yd) de la puerta, bastante más que la mitad del ancho total del arco. A veces, se logran disparos que hay que verlos para creerlos, tal como este tiro libre de Roberto Carlos ante Francia en la Copa Confederaciones en junio de 1997:



Roberto Carlos golpeó la bola con el borde externo de su pie izquierdo desde unos 32m (35yd) a unos 137km/h hacia el costado derecho de la barrera. Parecía que el balón iba a aterrizar tan lejos de la puerta que uno de los pasabolas se agachó para evitar el balonazo, pero cuando el balón se fue frenando, la magia de la fuerza de Magnus se hizo presente. Girando contra las manecillas del reloj, el balón curvó aún más hacia la izquierda y entró en el arco.

Otro gran ejemplo de este fenómeno es el disparo del sueco Mikael Nilsson en un partido entre su equipo, el IFK Göteborg y el PSV Eindhoven de la Champions League 92-93:



Así que ya saben, la práctica hace al maestro!